北航OO第一单元作业总结

前言

通过对表达式结构进行建模，完成多变量多项式的括号展开，初步体会层次化设计的思想。

然而我对自己的设计并不是很满意，当完成第三次作业的时候代码行数已经达到了993行。还有许多可以改进之处，在此进行总结。

第一次作业

题目简述

读入一个包含加、减、乘、乘方以及括号（其中括号的深度至多为 1 层）的多变量表达式，输出恒等变形展开所有括号后的表达式。

整体架构

我采用的是递归下降算法，先将表达式进行语法解析，再计算化简。根据课程提供的形式化表述，表达式解析为：

  • Expr：表达式及表达式因子
  • Term：项
  • ExprPow：表达式及对于指数
  • Number：常数因子
  • Power：变量因子

具体的类图如下：

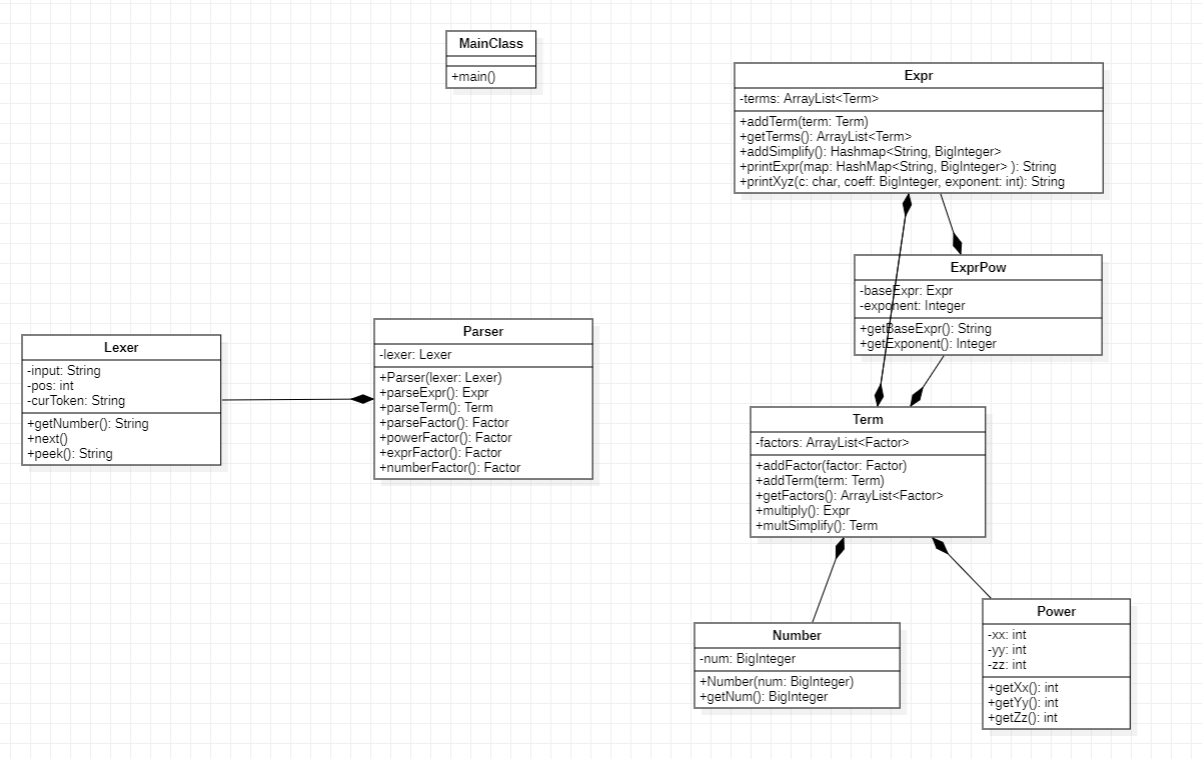
image-20230317163205842

架构解析

本次作业可以分为三个部分，第一个是表达式模型，第二个是表达式解析，第三个是表达式化简。

表达式模型

根据题目提供的形式化表述(摘录部分)：

表达式 → 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项

项 → [加减 空白项] 因子 | 项 空白项 ‘*’ 空白项 因子

因子 → 变量因子 | 常数因子 | 表达式因子

变量因子 → 幂函数

常数因子 → 带符号的整数

表达式因子 → ‘(’ 表达式 ‘)’ [空白项 指数]

幂函数 → (‘x’ | ‘y’ | ‘z’) [空白项 指数]

表达式由项组成（用 Arraylist 存储项，加减合并到项中）；项由三类因子组成，这里使用了 Factor 接口，首个因子前的加减作为一个因子存入项中；变量因子、常熟因子、表达式因子分别为 Power ，Number， Expr类中。

表达式解析

语法分析主要参考了OO课程组发布的预习文章中的递归下降算法的代码。Lexer类实现词法分析，实现加减、变量、数字等基本单元的提取。Parser 类对表达式进行语法分析，主要采用递归调用的方法。

表达式化简

由于不存在嵌套括号，表达式即为 A+B+...+ZA+B+...+Z （其中A, B, …, Z为项）的形式，可以先将项进行乘法展开，再进行加法。另外注意到化简完的式子均形如 A*x**B*y**C*z**D (A, B, C, D 均为常数)，在进行乘法化简的时候只需要统计项中 A, B, C, D的值，在进行加法化简的时候可以考虑使用 HashMap<key, value>, key应为 xx, yy, zz的指数的键值对，可应用 key=(String)(B|C|D) （这样可以避免重写 HashMap 的 equals 和 hashcode 方法）。

注意点

  1. 如何处理空白字符及符号问题？

    对于空白字符，由于本次作业不需要我们判断输入的合法性，所以对于输入的字符串 input ，直接过滤掉所有空白字符：

    input = input.replaceAll("[ \t]", "");

    对于符号，我们注意到：①常数因子带符号；②在项的第一个因子前可以带一个正负号；③在表达式的第一项之前可以带一个正负号；④表达式中项与项之间的加减号。 在出现符号的相应位置，如果是 -，就转化为项中的一个 −1-1 的常数因子，例如 -x=-1*x ；如果是 +，忽略即可。同时我们也可以预处理连续的 +- 和 *+ 等情况进行优化。

  2. 如何处理 表达式因子 → ‘(’ 表达式 ‘)’ [空白项 指数] ？

    我在 Training 给的模板的基础上新增了 ExprPow 类。在语法分析时，当项中读到了 ExprPow 类的因子，就把其展开为 Expr*Expr*…*Expr 。

    public class ExprPow implements Factor {
        private Expr baseExpr;
        private Integer exponent;
    }

  3. 注意细节

    例如，0\*\*0=1 ，其中，前者的 0 可以为满足题意的任意表达式因子化简后的结果。

性能优化

对比最冗余的输出，除了在上文表达式化简中提及的同类项合并外，可以考虑优化项为0，项的系数为1，变量的指数为0或1等的情形，以下主要说明相对不易考虑到的两点：

  1. 由于表达式第一项的正负号可以省略，我们应尽量保证其为正的，此时我们可以考虑如果该项为负，就放到生成的字符串结果的末尾，如果为正，就放到生成的字符串结果的开头。然后判断字符串首字母是否为 +。
  2. x*x 比 x**2 更优。

复杂度分析

Expr.addSimplify() 15.0 1.0 6.0 6.0
Expr.addTerm(Term) 0.0 1.0 1.0 1.0
Expr.Expr() 0.0 1.0 1.0 1.0
Expr.getTerms() 0.0 1.0 1.0 1.0
Expr.printExpr(HashMap) 38.0 4.0 15.0 17.0
Expr.printXyz(char, BigInteger, int) 15.0 1.0 9.0 9.0
ExprPow.ExprPow(Expr, Integer) 0.0 1.0 1.0 1.0
ExprPow.getBaseExpr() 0.0 1.0 1.0 1.0
ExprPow.getExponent() 0.0 1.0 1.0 1.0
Lexer.getNumber() 2.0 1.0 3.0 3.0
Lexer.Lexer(String) 0.0 1.0 1.0 1.0
Lexer.next() 7.0 2.0 5.0 6.0
Lexer.peek() 0.0 1.0 1.0 1.0
MainClass.main(String[]) 18.0 3.0 11.0 12.0
Number.getNum() 0.0 1.0 1.0 1.0
Number.Number(BigInteger) 0.0 1.0 1.0 1.0
Parse.exprFactor() 5.0 3.0 3.0 3.0
Parse.numberFactor() 11.0 1.0 8.0 8.0
Parse.Parse(Lexer) 0.0 1.0 1.0 1.0
Parse.parseExpr() 7.0 1.0 7.0 7.0
Parse.parseFactor() 4.0 1.0 5.0 5.0
Parse.parseTerm() 11.0 1.0 6.0 6.0
Parse.powerFactor() 24.0 9.0 6.0 9.0
Power.add(int, int, int) 0.0 1.0 1.0 1.0
Power.getXx() 0.0 1.0 1.0 1.0
Power.getYy() 0.0 1.0 1.0 1.0
Power.getZz() 0.0 1.0 1.0 1.0
Power.Power(int, int, int) 0.0 1.0 1.0 1.0
Term.addFactor(Factor) 0.0 1.0 1.0 1.0
Term.addTerm(Term) 0.0 1.0 1.0 1.0
Term.getFactors() 0.0 1.0 1.0 1.0
Term.multiply() 34.0 1.0 11.0 11.0
Term.multsimplify(Term) 4.0 1.0 3.0 3.0
Term.Term() 0.0 1.0 1.0 1.0
Total 195.0 50.0 118.0 125.0
Average 5.735294117647059 1.4705882352941178 3.4705882352941178 3.676470588235294

由于输出字符串全都集中在了Expr 类的 printExpr 方法中，复杂度较高；由于 power 类中存储的是 x, y, z 的次数，导致 Parse 类的 PowerFactor方法复杂度较高；在乘法计算时，由于一开始写的是先完全进行乘法展开再合并同类项，发现容易爆栈，于是直接在此基础上进行了修改，复杂度也比较高。

bug 分析

本次作业遇到的bug主要是先完全进行乘法展开再合并同类项，发现容易爆栈，于是改成了在处理项的过程中就插入同类项合并操作。

总结

虽然本次作业强测满分，互测没有被 hack，但整体的架构还是不太满意的，比如不支持括号嵌套，对 power的处理比较复杂，字符串输出难以迭代。这些都在后面的作业中有修改。

第二次作业

题目简述

读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用的表达式，输出恒等变形展开所有括号后的表达式。

整体架构

本次我才用了 边分析边化简 的方法，比起第一次作业采用的先分析后化简明显是有利的。

迭代内容

对于表达式解析，新增了 Trigon 类存储三角函数（然而我的 Expr , ExprPow, Trigon 类是可以合并的）。

新增了 CusFuncProcess 和 CusFunction 来处理自定义函数因子。

重载 equals 方法判断表达式是否相等，重载 toString 方法返回字符串。

具体的类图如下：

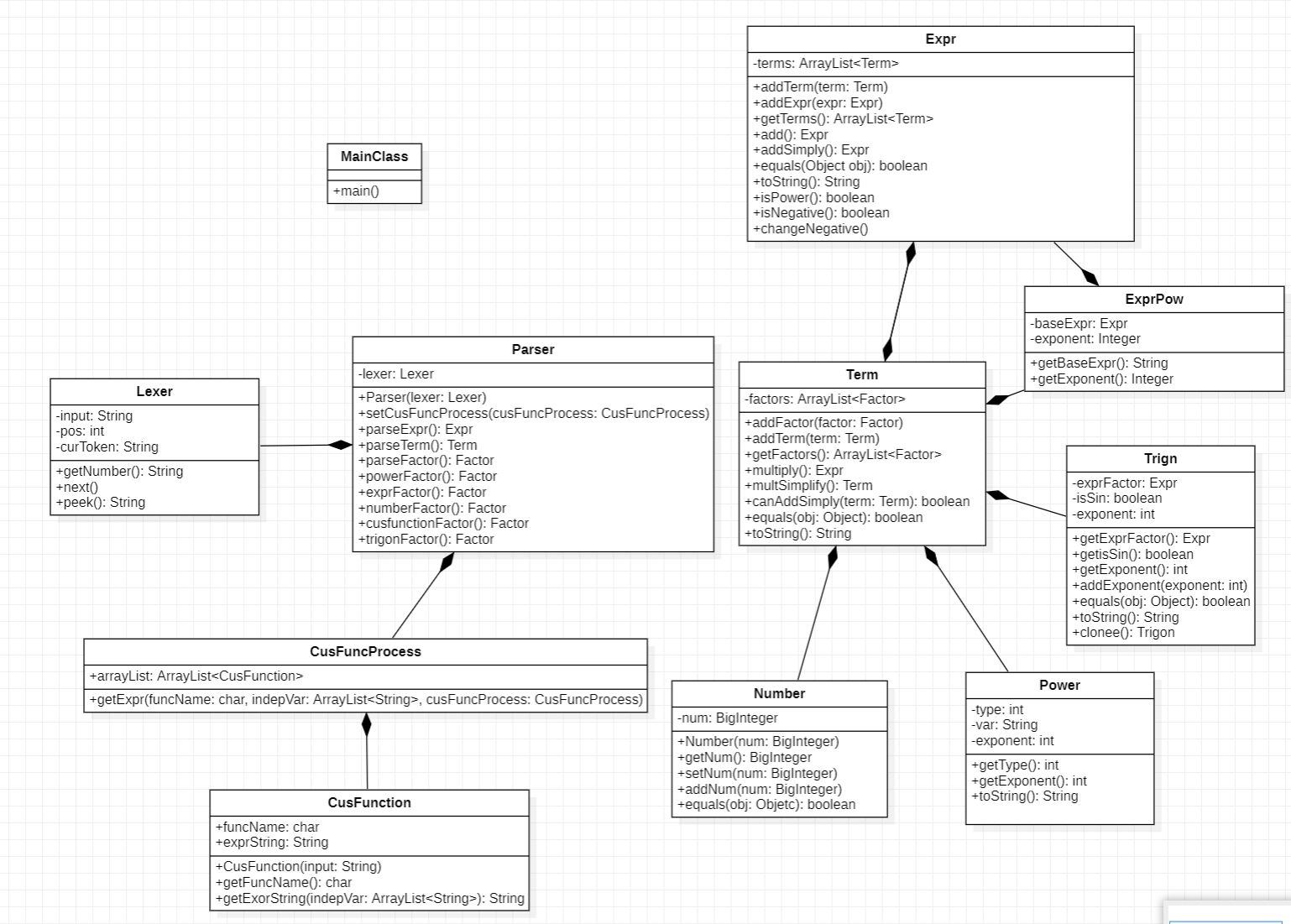
image-20230318103340317

对于新增的类和方法：

  • Trigon：三角函数因子
  • CusFunction：自变量函数
  • CusFuncProcess：自变量函数集合

关键问题

在第一次作业的基础上迭代，主要考虑以下问题：

  1. 括号嵌套处理

    修改了计算化简部分的方法，处理上应该不会有太大问题。

  2. 三角函数处理

    在语法分析时，三角函数因子的处理方式和其他因子相似。

    在计算化简时，由于其独特的属性会带来一些不同，会在“性能优化”部分详细描述。

  3. 自定义函数调用

    考虑到方法撰写的难度和时间、空间上的消耗，对于读入的自定义函数，先进行预处理：①对自定义函数用语法树分析一遍，再转为字符串；②将自定义函数中的形参按顺序用例如 u , v , w 等未出现的字母 replaceAll （原因请读者自己思考）。

    当在所求的表达式中遇到自定义函数，将实参代入后再分析即可。这里值得注意的一点是在所求表达式中遇到形如 f(A,B,C)f(A, B, C) ，如何取出实参？有多种做法，我采用的是用 Parser 取出实参 exprA , exprB , exprC ，再转化为字符串，代入自定义函数字符串。那么此时我们又会遇到一个问题：若

    11

    f(x)=x∗sin(x)f(x)=x*sin(x)

    f(y+sin(x))f(y+sin(x))

    如果按上述方法，我们会得到 y+sin(x)/∗/∗2y+sin(x)/*/*2 ，显然是有问题的。此时我们可以采用 "(" + expr.toString() + ")" 代入自定义函数字符串。

性能优化

我们注意到最终表达式的每一项形如 A*x**B*y**C*z**D*[sin(expr)**E][cos(expr)**F]$ ( $[]$ 表示这一项可以省略)。

  • 在 multSimplify 中，把每一项都化简成上述形式，其中三角函数的合并同类项需要判断 expr 是否相等（重载equals），如果相等指数相加（新开一个 Trigon 保存！！！）。
  • 在 addSimplify 中，判断项与项是否相同（此处相同指除了系数 AA 外均相同），相同则 A=A1+A2A=A_1+A_2 ， 其余不变。
  • sin(0)=0,cos(0)=1sin(0)=0, cos(0)=1
  • sin(−A)=−A,cos(−A)=Asin(-A)=-A, cos(-A)=A
  • 三角函数对应的嵌套因子为不带指数的表达式因子时，该表达式因子两侧必要的一层括号；否则可省略。
  • 表达式尽量保证首项是正的。

复杂度分析

CusFuncProcess.CusFuncProcess(ArrayList) 3.0 1.0 3.0 3.0
CusFuncProcess.getExpr(char, ArrayList, CusFuncProcess) 3.0 1.0 3.0 3.0
CusFunction.CusFunction(String) 2.0 1.0 3.0 3.0
CusFunction.getExprString(ArrayList) 2.0 1.0 3.0 3.0
CusFunction.getFuncName() 0.0 1.0 1.0 1.0
Expr.add() 1.0 1.0 2.0 2.0
Expr.addExpr(Expr) 0.0 1.0 1.0 1.0
Expr.addSimply() 8.0 1.0 5.0 5.0
Expr.addTerm(Term) 0.0 1.0 1.0 1.0
Expr.changeNegative() 1.0 1.0 2.0 2.0
Expr.equals(Object) 16.0 6.0 5.0 8.0
Expr.Expr() 0.0 1.0 1.0 1.0
Expr.getTerms() 0.0 1.0 1.0 1.0
Expr.isNegative() 3.0 3.0 2.0 3.0
Expr.isPower() 19.0 7.0 6.0 11.0
Expr.toString() 8.0 1.0 7.0 7.0
ExprPow.ExprPow(Expr, Integer) 0.0 1.0 1.0 1.0
ExprPow.getBaseExpr() 0.0 1.0 1.0 1.0
ExprPow.getExponent() 0.0 1.0 1.0 1.0
Lexer.getNumber() 2.0 1.0 3.0 3.0
Lexer.getPos() 0.0 1.0 1.0 1.0
Lexer.Lexer(String) 0.0 1.0 1.0 1.0
Lexer.next() 11.0 2.0 9.0 10.0
Lexer.peek() 0.0 1.0 1.0 1.0
MainClass.initString(String) 18.0 3.0 11.0 12.0
MainClass.main(String[]) 1.0 1.0 2.0 2.0
Number.addNum(BigInteger) 0.0 1.0 1.0 1.0
Number.equals(Object) 5.0 4.0 3.0 4.0
Number.getNum() 0.0 1.0 1.0 1.0
Number.Number(BigInteger) 0.0 1.0 1.0 1.0
Number.setNum(BigInteger) 0.0 1.0 1.0 1.0
Parse.cusfunctionFactor() 6.0 3.0 4.0 5.0
Parse.exprFactor() 5.0 3.0 3.0 3.0
Parse.numberFactor() 11.0 1.0 8.0 8.0
Parse.Parse(Lexer) 0.0 1.0 1.0 1.0
Parse.parseExpr() 7.0 1.0 7.0 7.0
Parse.parseFactor() 8.0 1.0 10.0 10.0
Parse.parseTerm() 11.0 1.0 6.0 6.0
Parse.powerFactor() 24.0 9.0 6.0 9.0
Parse.setCusFuncProcess(ArrayList) 0.0 1.0 1.0 1.0
Parse.setCusFuncProcess(CusFuncProcess) 0.0 1.0 1.0 1.0
Parse.trigonFactor() 19.0 7.0 7.0 9.0
Power.equals(Object) 6.0 4.0 4.0 5.0
Power.getExponent() 0.0 1.0 1.0 1.0
Power.getType() 0.0 1.0 1.0 1.0
Power.Power(int, int) 3.0 1.0 1.0 3.0
Power.toString() 3.0 1.0 3.0 3.0
Term.addFactor(Factor) 0.0 1.0 1.0 1.0
Term.addTerm(Term) 0.0 1.0 1.0 1.0
Term.canAddsimply(Term) 14.0 7.0 3.0 8.0
Term.equals(Object) 16.0 6.0 5.0 8.0
Term.getFactors() 0.0 1.0 1.0 1.0
Term.multiply() 30.0 1.0 10.0 10.0
Term.multSimply() 22.0 1.0 11.0 11.0
Term.Term() 0.0 1.0 1.0 1.0
Term.toString() 40.0 6.0 15.0 17.0
Trigon.addExponent(int) 0.0 1.0 1.0 1.0
Trigon.clonee() 0.0 1.0 1.0 1.0
Trigon.equals(Object) 6.0 4.0 5.0 6.0
Trigon.getExponent() 0.0 1.0 1.0 1.0
Trigon.getExprFactor() 0.0 1.0 1.0 1.0
Trigon.getisSin() 0.0 1.0 1.0 1.0
Trigon.toString() 8.0 1.0 5.0 8.0
Trigon.Trigon(Expr, boolean, int) 0.0 1.0 1.0 1.0
Total 342.0 123.0 212.0 247.0
Average 5.34375 1.921875 3.3125 3.859375
ExprPow 1.0 1.0 3.0
Number 1.6 4.0 8.0
Trigon 2.25 8.0 18.0
CusFunction 2.3333333333333335 3.0 7.0
Lexer 2.4 7.0 12.0
Power 2.4 4.0 12.0
CusFuncProcess 3.0 3.0 6.0
Expr 3.6363636363636362 10.0 40.0
Parse 4.636363636363637 9.0 51.0
MainClass 6.0 10.0 12.0
Term 6.222222222222222 16.0 56.0
Total 225.0
Average 3.515625 6.818181818181818 20.454545454545453

由于先完成作业基本要求，再思考性能优化，以及 ArrayList 的局限性，优化函数写的比较冗余；Expr，Term等类聚集了比较多的功能。

bug 分析

在评测时，遇到一个bug是因为在合并同类项时没有进行深拷贝，直接在原项上加减，导致对该项出现在的其他位置产生了影响。

总结

对于第二次作业，我在第一次作业的基础上进行了大幅度的修改，仅保留了第一次作业的语法分析。并且感觉本次作业写的比较冗余，可能不利于第三次迭代。个人建议是在写之前，列清楚每个类、属性、方法的用处，调用关系等，而不是边写边扩充（其实我的代码里有些都是可以合并的）。

第三次作业

题目简述

读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用、求导算子的表达式，输出恒等变形展开所有括号后的表达式。

整体架构

迭代内容

  • 加入求导算子，解决方法是在每个表达式模型的类中加入 differentiate 方法。
  • 自定义函数表达式支持调用其他已已定义的函数，由于在第二次作业中我对自定义函数的处理是先对其语法分析，将结果存为字符串，再传给表达式语法分析的 Parse 类，进行自变量替换，已经支持该功能，几乎不需要做改动。

具体的类图如下：

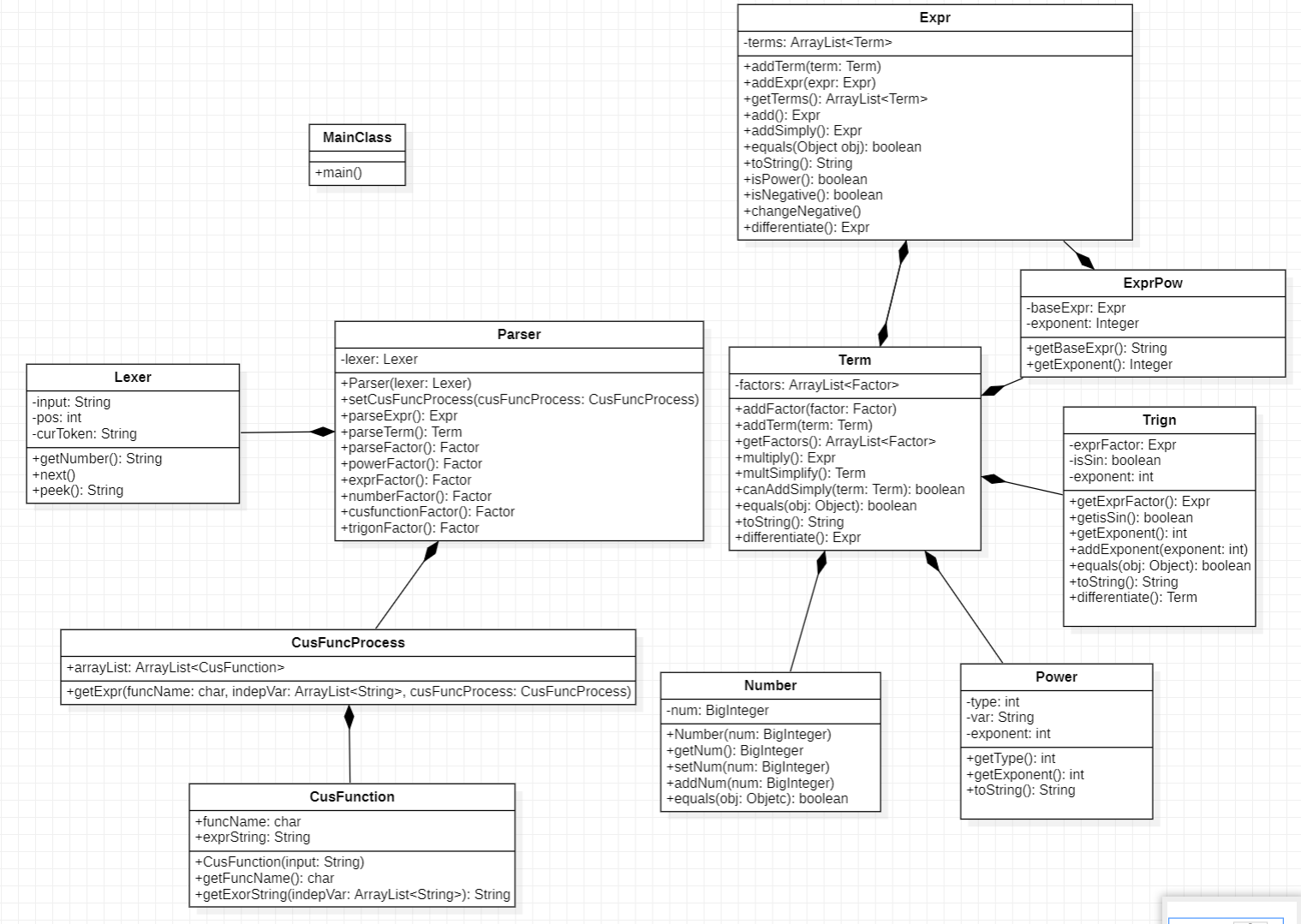
image-20230318105523253

与第二次作业对比，仅在 Expr, Term, Trigon 类里加了求导方法。

复杂度分析

CusFuncProcess.addCusFuncProcess(String) 0.0 1.0 1.0 1.0
CusFuncProcess.getExpr(char, ArrayList, CusFuncProcess) 3.0 1.0 3.0 3.0
CusFunction.CusFunction(String, CusFuncProcess) 2.0 1.0 3.0 3.0
CusFunction.getExprString(ArrayList) 2.0 1.0 3.0 3.0
CusFunction.getFuncName() 0.0 1.0 1.0 1.0
Expr.add() 1.0 1.0 2.0 2.0
Expr.addAllTerms(Expr) 1.0 1.0 2.0 2.0
Expr.addSimplify() 12.0 1.0 6.0 6.0
Expr.addTerm(Term) 1.0 1.0 2.0 2.0
Expr.changeNegative() 1.0 1.0 2.0 2.0
Expr.clone() 1.0 1.0 2.0 2.0
Expr.differentiate(String) 4.0 2.0 3.0 4.0
Expr.diffIsZero(String) 1.0 2.0 1.0 2.0
Expr.equals(Object) 16.0 6.0 5.0 8.0
Expr.Expr() 0.0 1.0 1.0 1.0
Expr.getTerms() 0.0 1.0 1.0 1.0
Expr.isNegative() 3.0 3.0 2.0 3.0
Expr.isPower() 16.0 7.0 6.0 11.0
Expr.toString() 8.0 1.0 7.0 7.0
ExprPow.clone() 0.0 1.0 1.0 1.0
ExprPow.ExprPow(Expr, Integer) 0.0 1.0 1.0 1.0
ExprPow.getBaseExpr() 0.0 1.0 1.0 1.0
ExprPow.getExponent() 0.0 1.0 1.0 1.0
Lexer.getNumber() 2.0 1.0 3.0 3.0
Lexer.getPos() 0.0 1.0 1.0 1.0
Lexer.Lexer(String) 0.0 1.0 1.0 1.0
Lexer.next() 11.0 2.0 9.0 10.0
Lexer.peek() 0.0 1.0 1.0 1.0
MainClass.initString(String) 18.0 3.0 11.0 12.0
MainClass.main(String[]) 1.0 1.0 2.0 2.0
Number.addNum(BigInteger) 0.0 1.0 1.0 1.0
Number.clone() 0.0 1.0 1.0 1.0
Number.equals(Object) 5.0 4.0 3.0 4.0
Number.getNum() 0.0 1.0 1.0 1.0
Number.Number(BigInteger) 0.0 1.0 1.0 1.0
Number.setNum(BigInteger) 0.0 1.0 1.0 1.0
Parse.cusfunctionFactor() 6.0 3.0 4.0 5.0
Parse.derivativeFactor() 1.0 1.0 2.0 2.0
Parse.exprFactor() 5.0 3.0 3.0 3.0
Parse.numberFactor() 11.0 1.0 8.0 8.0
Parse.Parse(Lexer) 0.0 1.0 1.0 1.0
Parse.parseExpr() 7.0 1.0 7.0 7.0
Parse.parseFactor() 9.0 1.0 11.0 11.0
Parse.parseTerm() 11.0 1.0 6.0 6.0
Parse.powerFactor() 24.0 9.0 6.0 9.0
Parse.setCusFuncProcess(CusFuncProcess) 0.0 1.0 1.0 1.0
Parse.trigonFactor() 19.0 7.0 7.0 9.0
Power.clone() 0.0 1.0 1.0 1.0
Power.equals(Object) 6.0 4.0 4.0 5.0
Power.getExponent() 0.0 1.0 1.0 1.0
Power.getType() 0.0 1.0 1.0 1.0
Power.Power(String, int) 0.0 1.0 1.0 1.0
Power.toString() 3.0 1.0 3.0 3.0
Term.addAllFactors(Term) 1.0 1.0 2.0 2.0
Term.addFactor(Factor) 1.0 1.0 2.0 2.0
Term.canAddSimplify(Term) 14.0 7.0 3.0 8.0
Term.clone() 1.0 1.0 2.0 2.0
Term.differentiate(String) 30.0 11.0 9.0 14.0
Term.equals(Object) 16.0 6.0 5.0 8.0
Term.getFactors() 0.0 1.0 1.0 1.0
Term.multiply() 34.0 1.0 11.0 11.0
Term.multSimplify() 23.0 2.0 11.0 12.0
Term.Term() 0.0 1.0 1.0 1.0
Term.toString() 40.0 6.0 14.0 16.0
Trigon.clone() 0.0 1.0 1.0 1.0
Trigon.differentiate(String) 3.0 1.0 3.0 3.0
Trigon.equals(Object) 6.0 4.0 5.0 6.0
Trigon.getExponent() 0.0 1.0 1.0 1.0
Trigon.getExprFactor() 0.0 1.0 1.0 1.0
Trigon.getisSin() 0.0 1.0 1.0 1.0
Trigon.toString() 8.0 1.0 5.0 8.0
Trigon.Trigon(Expr, boolean, int) 0.0 1.0 1.0 1.0
Total 388.0 144.0 239.0 280.0
Average 5.388888888888889 2.0 3.3194444444444446 3.888888888888889
ExprPow 1.0 1.0 4.0
Number 1.5 4.0 9.0
Power 1.8333333333333333 4.0 11.0
CusFuncProcess 2.0 3.0 4.0
CusFunction 2.3333333333333335 3.0 7.0
Lexer 2.4 7.0 12.0
Trigon 2.5 8.0 20.0
Expr 3.642857142857143 10.0 51.0
Parse 4.818181818181818 9.0 53.0
MainClass 6.0 10.0 12.0
Term 6.818181818181818 15.0 75.0
Total 258.0
Average 3.5833333333333335 6.7272727272727275 23.454545454545453

这次的一些类复杂度高的原因其实和上次作业相同，因为担心改了出问题，所以并没有改动架构。

bug 分析

本次作业遇到的bug是求导时，如果因子不含有求导变量，会返回null，然后出现了 −dx(2)=1-dx(2) = 1。在提交强测前已自检出。

第一单元作业总结

本单元作业结果上是ok的，但是架构上不太合适，比如可扩展性不太好，一些类复杂度比较高，一些可以复合的地方写的比较冗余。在以后的作业中，我觉得需要提前为下一次迭代预留空间，先思考好每个要求由哪些类实现，每个类实现哪些功能，减少类与类之间的耦合度。

如果发现写的有误或有更好的做法，欢迎到评论区指正或分享 (*^▽^*)